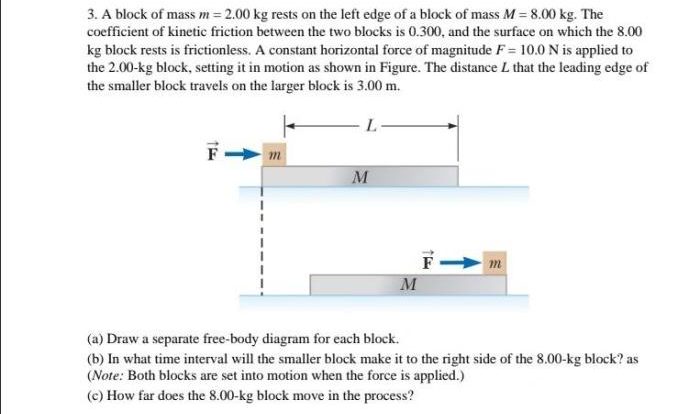
A ball of mass m swings in a horizontal circle, showcasing the interplay of fundamental physics principles. This motion involves the delicate balance between mass, centripetal force, tangential velocity, and energy transformations.
As the ball traverses its circular path, its mass influences the magnitude of the centripetal force required to maintain its trajectory. This force, directed towards the center of the circle, ensures that the ball remains in its circular path despite its tangential velocity, which is perpendicular to the radius vector.
Mass and Circular Motion: A Ball Of Mass M Swings In A Horizontal Circle
The mass of the ball plays a significant role in its circular motion. A larger mass results in a greater centripetal force required to keep the ball moving in a circle. This is because centripetal force is directly proportional to mass.
Conversely, a smaller mass requires a smaller centripetal force.
Mass also influences the ball’s tangential velocity. Tangential velocity is the velocity of the ball in the direction tangent to the circle. A larger mass will have a smaller tangential velocity for the same centripetal force, while a smaller mass will have a larger tangential velocity.
The trajectory of the ball in a circular path is affected by its mass. A larger mass will have a smaller radius of curvature for the same tangential velocity, while a smaller mass will have a larger radius of curvature.
Centripetal Force

Centripetal force is the force that acts towards the center of a circle and keeps the ball moving in a circular path. It is given by the equation:
Fc= mv 2/r
where F cis the centripetal force, m is the mass of the ball, v is the tangential velocity of the ball, and r is the radius of the circle.
The magnitude of the centripetal force is determined by the mass of the ball, the tangential velocity of the ball, and the radius of the circle. A larger mass, a larger tangential velocity, or a smaller radius of curvature will result in a larger centripetal force.
Tangential Velocity
Tangential velocity is the velocity of the ball in the direction tangent to the circle. It is given by the equation:
v = rω
where v is the tangential velocity, r is the radius of the circle, and ω is the angular velocity of the ball.
The tangential velocity of the ball is related to the centripetal force by the equation:
Fc= mv 2/r
This equation shows that the tangential velocity of the ball is directly proportional to the centripetal force.
Circular Motion Equations

The following equations are used to describe circular motion:
- Centripetal force equation: F c= mv 2/r
- Tangential velocity equation: v = rω
- Angular velocity equation: ω = v/r
These equations can be used to analyze the motion of a ball swinging in a horizontal circle.
Energy Considerations
During circular motion, the ball’s kinetic energy and potential energy are constantly changing. At the top of the circle, the ball has maximum potential energy and zero kinetic energy. At the bottom of the circle, the ball has maximum kinetic energy and zero potential energy.
The total energy of the ball is conserved throughout its motion. This means that the sum of the kinetic energy and potential energy is constant.
Applications
The principles of a ball swinging in a horizontal circle are applied in a variety of real-world situations, including:
- Engineering: Centripetal force is used to keep objects moving in a circular path in a variety of engineering applications, such as centrifuges and amusement park rides.
- Sports: Centripetal force is responsible for the curved trajectory of a thrown ball or a batted baseball.
- Other fields: Centripetal force is also used in a variety of other fields, such as physics, astronomy, and meteorology.
Key Questions Answered
What is the centripetal force acting on the ball?
The centripetal force is given by the equation Fc = mv^2/r, where m is the mass of the ball, v is its tangential velocity, and r is the radius of the circle.
How does the mass of the ball affect its circular motion?
The mass of the ball affects the magnitude of the centripetal force required to keep it in circular motion. A heavier ball requires a greater centripetal force to maintain the same circular path.
What is the relationship between tangential velocity and centripetal force?
Tangential velocity is perpendicular to the radius vector and represents the ball’s speed along the circular path. Centripetal force is directed towards the center of the circle and provides the necessary inward force to keep the ball moving in a circular path.