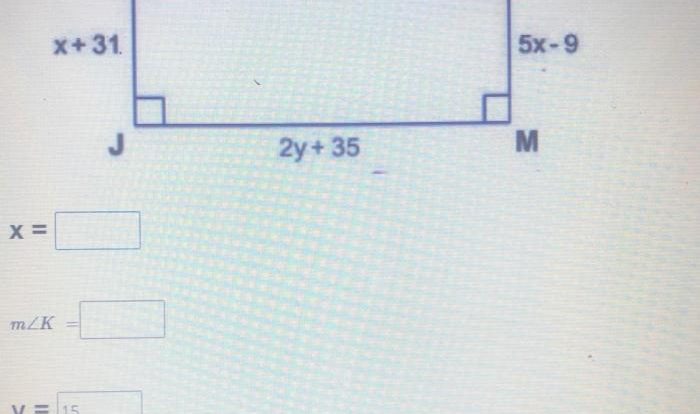
Angles of polygons scavenger hunt answer key: Dive into the fascinating world of polygons and unravel the secrets of their angles through an engaging scavenger hunt. This guide provides a comprehensive overview of the types, properties, and applications of polygon angles, equipping you with the knowledge to conquer any angle-related challenge.

From understanding the intricacies of interior and exterior angles to calculating the sum of interior angles, this guide delves into the fundamental concepts of polygon angles. It explores the unique characteristics of specific polygons, such as triangles, squares, and pentagons, and unravels the practical applications of polygon angle properties in fields like architecture and engineering.

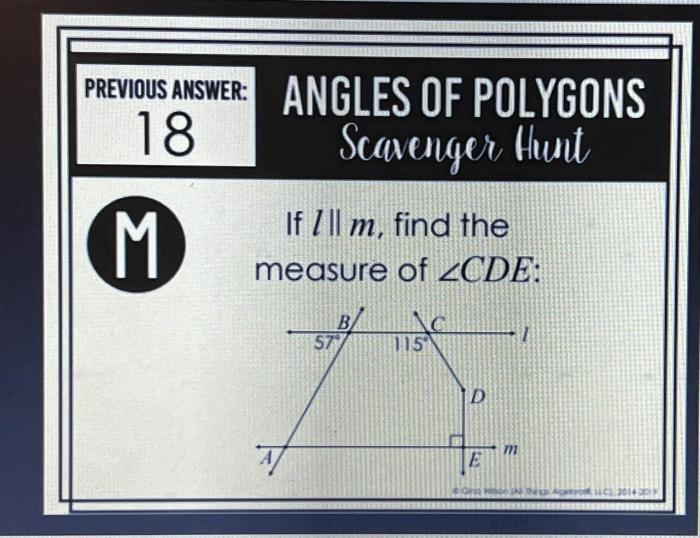
Angles of Polygons: Angles Of Polygons Scavenger Hunt Answer Key

Polygons are two-dimensional shapes with straight sides and angles. Understanding the angles of polygons is crucial in geometry, as they play a significant role in determining the shape and properties of these figures.

Types of Angles in Polygons

There are two main types of angles in polygons: interior angles and exterior angles.

• Interior anglesare the angles formed inside the polygon, at the intersection of two sides.
• Exterior anglesare the angles formed outside the polygon, adjacent to one side and one vertex.

Interior angles can be classified into:

• Acute angles: Angles less than 90 degrees.
• Obtuse angles: Angles greater than 90 degrees but less than 180 degrees.
• Right angles: Angles exactly equal to 90 degrees.
• Straight angles: Angles exactly equal to 180 degrees.

Angle Sum Properties of Polygons, Angles of polygons scavenger hunt answer key

The angle sum property of polygons states that the sum of the interior angles of a polygon with nsides is given by the formula: ( n– 2) × 180 degrees.

For example, the sum of the interior angles of a triangle ( n= 3) is (3 – 2) × 180 = 180 degrees, and the sum of the interior angles of a quadrilateral ( n= 4) is (4 – 2) × 180 = 360 degrees.

Angles of Specific Polygons

• Triangle: 3 sides, 3 angles, each interior angle is 60 degrees.
• Square: 4 sides, 4 angles, each interior angle is 90 degrees.
• Rectangle: 4 sides, 4 angles, opposite interior angles are equal and each interior angle is 90 degrees.
• Pentagon: 5 sides, 5 angles, each interior angle is 108 degrees.

Applications of Polygon Angle Properties

Polygon angle properties have numerous applications in fields such as:

• Architecture: Determining the angles of roofs, windows, and other structural elements.
• Engineering: Calculating the angles of bridges, trusses, and other load-bearing structures.
• Design: Creating aesthetically pleasing shapes and patterns in graphic design, interior design, and other creative fields.

Essential FAQs

What is the angle sum property for a polygon?

The angle sum property states that the sum of the interior angles of a polygon with n sides is (n-2) – 180 degrees.

How do I calculate the measure of an interior angle in a regular polygon?

To calculate the measure of an interior angle in a regular polygon, divide the sum of the interior angles by the number of sides.

What are the applications of polygon angle properties in real-world scenarios?

Polygon angle properties find applications in architecture, engineering, and design, helping determine the shape and structure of objects and ensuring stability and functionality.