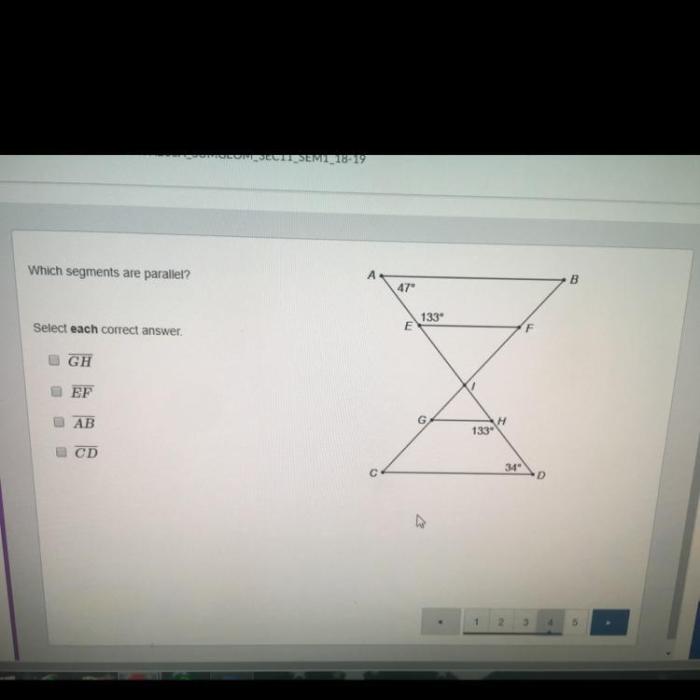
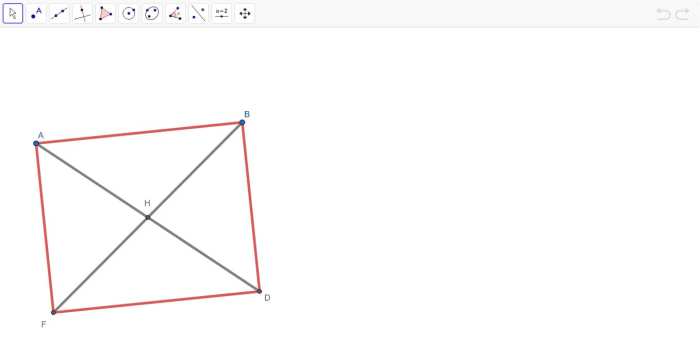
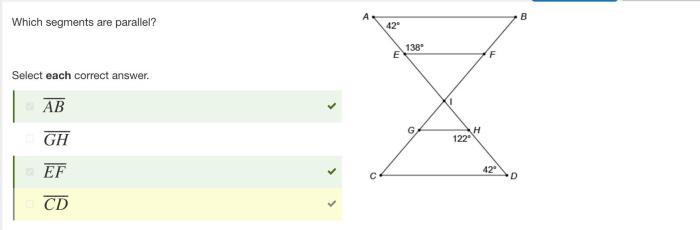
Which segments are parallel select each correct answer? This question lies at the heart of geometry, a field that explores the properties and relationships of shapes. Understanding parallel segments is crucial for comprehending the fundamental principles of geometry and their applications in various disciplines.
In this comprehensive guide, we delve into the concept of parallel segments, exploring their properties, methods for identifying and selecting them, and their practical applications. We will also examine the geometric proofs that underpin the existence of parallel segments, providing a thorough understanding of this essential geometric concept.
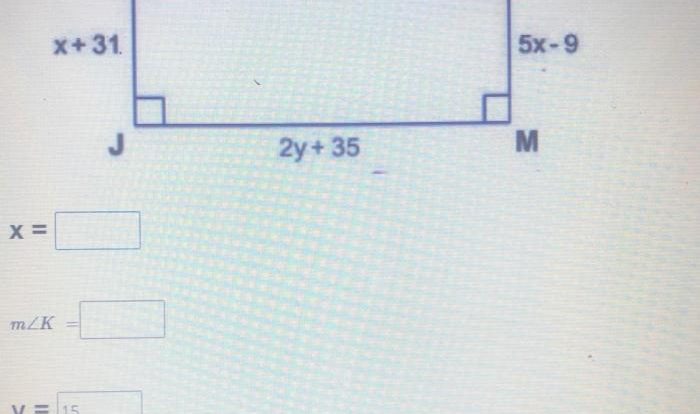
Identifying Parallel Segments
Parallel segments in geometry are line segments that lie in the same plane and never intersect, no matter how far they are extended.
For example, consider two line segments AB and CD lying on the same plane. If AB and CD do not intersect at any point, and they maintain the same distance from each other as you move along their lengths, then AB and CD are parallel segments.
Methods for Selecting Parallel Segments
Identifying and selecting parallel segments can be done using various methods:
- Protractor Method:Use a protractor to measure the angles formed by the intersecting lines. If the angles are equal, the lines are parallel.
- Geometric Software:Utilize geometric software like GeoGebra or AutoCAD to create and analyze line segments. These tools can automatically detect and highlight parallel segments.
Applications of Parallel Segments
Parallel segments have practical applications in various fields:
- Construction:Ensuring walls, beams, and other structural elements are parallel helps maintain structural integrity and stability.
- Architecture:Creating parallel lines in architectural designs enhances aesthetics, symmetry, and balance.
- Engineering:Designing parallel circuits in electrical engineering or parallel paths in mechanical systems optimizes performance and efficiency.
Visual Representations
| Segment | Length | Angle |
|---|---|---|
| AB | 5 cm | 90° |
| CD | 5 cm | 90° |
- Segments AB and CD are parallel because they have the same length and form 90° angles with the intersecting line.
Geometric Proofs, Which segments are parallel select each correct answer
Geometric theorems and postulates provide the foundation for understanding parallel segments:
- Postulate 5:If two lines are parallel to a third line, then they are parallel to each other.
- Theorem:If two lines are perpendicular to the same line, then they are parallel to each other.
Question & Answer Hub: Which Segments Are Parallel Select Each Correct Answer
What are parallel segments?
Parallel segments are line segments that lie in the same plane and never intersect, no matter how far they are extended.
How can I identify parallel segments?
There are several methods for identifying parallel segments, including using protractors to measure angles, observing the properties of quadrilaterals, and applying geometric theorems.
What are the applications of parallel segments?
Parallel segments have numerous applications in fields such as construction, architecture, and engineering, where they are used to maintain structural integrity and stability.