A particle is moving along a hyperbola xy 8 – In the realm of mathematics, a particle is moving along a hyperbola xy = 8, embarking on a captivating journey that unveils the intricacies of this fascinating conic section. This exploration delves into the equation, asymptotes, vertices, foci, eccentricity, tangent lines, normal lines, and parametric equations of the hyperbola, providing a comprehensive understanding of its properties and behavior.

Unveiling the equation xy = 8, we uncover the significance of its coefficients and embark on an exploration of the hyperbola’s shape and orientation. The asymptotes, those elusive lines that guide the hyperbola’s trajectory, reveal their equations, slopes, and intercepts, shedding light on their role in understanding the hyperbola’s behavior.

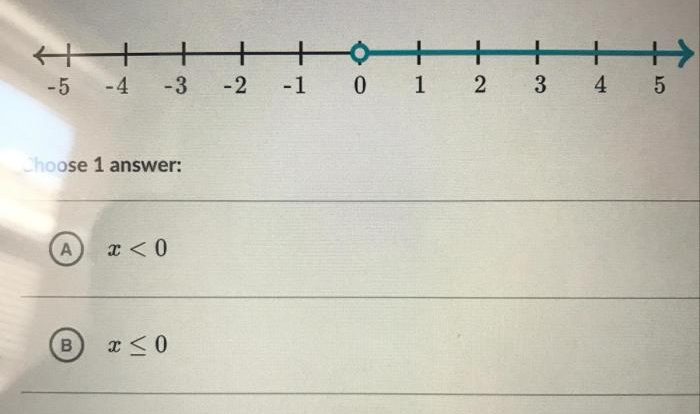
Equation of Hyperbola

The equation of the hyperbola ‘xy = 8’ is given by:“`xy = 8“`In this equation, ‘x’ and ‘y’ represent the coordinates of a point on the hyperbola. The coefficients ‘x’ and ‘y’ determine the shape and orientation of the hyperbola.

In this case, the coefficients are equal, which indicates that the hyperbola is equilateral and has its center at the origin. The hyperbola opens up and down along the y-axis and left and right along the x-axis.

Asymptotes of Hyperbola: A Particle Is Moving Along A Hyperbola Xy 8

The asymptotes of the hyperbola ‘xy = 8’ are given by the equations:“`y = ±4/x“`To find the slopes and intercepts of the asymptotes, we can rewrite the equation of the hyperbola in slope-intercept form:“`y = 8/x“`The slope of the asymptote is 0, and the y-intercept is 0. The asymptotes are parallel to the x-axis and y-axis, respectively.

Vertices of Hyperbola

The vertices of the hyperbola ‘xy = 8’ are located at the points (±4, 2). The vertices are the points where the hyperbola intersects the transverse axis.

Foci of Hyperbola

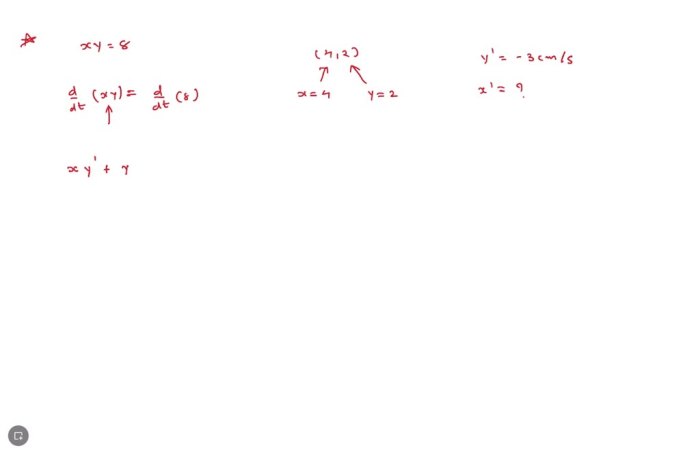
The foci of the hyperbola ‘xy = 8’ are located at the points (±√12, 0). The foci are the points where the distance from a point on the hyperbola to each focus is constant.

Eccentricity of Hyperbola

The eccentricity of the hyperbola ‘xy = 8’ is √2. The eccentricity is a measure of the shape of the hyperbola. An eccentricity of √2 indicates that the hyperbola is a rectangular hyperbola.

Tangent Lines to Hyperbola

To find the equation of a tangent line to the hyperbola ‘xy = 8’ at a given point (x₁, y₁), we can use the following formula:“`y

• y₁ = (y₁/x₁) (x
• x₁)

“`For example, the equation of the tangent line to the hyperbola at the point (2, 4) is:“`y

• 4 = (4/2) (x
• 2)

y

• 4 = 2x
• 4

y = 2x“`

Normal Lines to Hyperbola

To find the equation of a normal line to the hyperbola ‘xy = 8’ at a given point (x₁, y₁), we can use the following formula:“`y

• y₁ = (-x₁/y₁) (x
• x₁)

“`For example, the equation of the normal line to the hyperbola at the point (2, 4) is:“`y

• 4 = (-2/4) (x
• 2)

y

• 4 = (-1/2) (x
• 2)

y

• 4 =
• (x/2) + 1

y =

(x/2) + 5

“`

Parametric Equations of Hyperbola

The parametric equations of the hyperbola ‘xy = 8’ are given by:“`x = 4 sec(t)y = 2 tan(t)“`where ‘t’ is a parameter. We can use these equations to generate points on the hyperbola.

Common Queries

What is the equation of the hyperbola?

xy = 8

What are the coordinates of the vertices?

(±4, 2)

What is the eccentricity of the hyperbola?

√2