Moment of inertia of trapezium – The moment of inertia of a trapezium is a fundamental concept in physics that measures an object’s resistance to angular acceleration. It plays a crucial role in engineering and structural design, influencing the stability and motion of rotating objects.
This comprehensive guide delves into the intricacies of moment of inertia, exploring its formula, applications, and significance in rotational motion. We will also compare it to other geometric shapes to provide a deeper understanding of its unique properties.
Moment of Inertia Concepts
Moment of inertia is a physical quantity that describes the resistance of an object to angular acceleration. It is a measure of an object’s distribution of mass around its axis of rotation. The greater the moment of inertia, the more difficult it is to change the object’s angular velocity.The
formula for calculating the moment of inertia depends on the shape of the object. For a trapezium, the moment of inertia about an axis perpendicular to the plane of the trapezium and passing through the centroid is given by:“`I = (1/12)
- m
- (b1^2 + b2^2 + h^2)
“`where:* I is the moment of inertia
Understanding the moment of inertia of a trapezium is like studying the curious behavior of raccoons. Just as a group of raccoons is called a “gaze,” the moment of inertia quantifies an object’s resistance to rotational motion. Both concepts, though seemingly unrelated, share the fascination of exploring the dynamics of the physical world.
- m is the mass of the trapezium
- b1 and b2 are the lengths of the parallel sides of the trapezium
- h is the height of the trapezium
Moment of inertia is a crucial concept in physics, as it is used to determine the angular acceleration of an object when a torque is applied. It also plays a significant role in the design of rotating machinery, such as flywheels and turbines, where the moment of inertia is carefully controlled to achieve desired performance characteristics.
Moment of Inertia of Trapezium
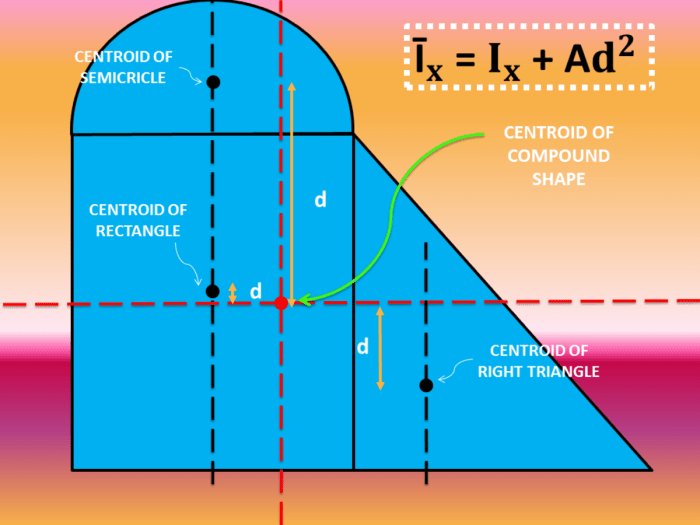
A trapezium is a quadrilateral with two parallel sides, known as bases, and two non-parallel sides. Let’s define the following geometric properties of a trapezium:
- a: Length of the shorter base
- b: Length of the longer base
- h: Height of the trapezium (perpendicular distance between the bases)
- I: Moment of inertia of the trapezium
The moment of inertia of a trapezium can be calculated using the following formula:
I = (1/12)
- m
- (a^2 + b^2 + h^2)
where:
- mis the mass of the trapezium
- aand bare the lengths of the shorter and longer bases, respectively
- his the height of the trapezium
The units of moment of inertia are kg-m^2.
Applications of Moment of Inertia

Moment of inertia finds extensive applications in engineering, particularly in structural design. It plays a crucial role in determining the stability and load-bearing capacity of structures.
Moment of Inertia in Structural Design
In structural design, moment of inertia is used to calculate the resistance of a structure to bending and twisting forces. A higher moment of inertia indicates a greater resistance to deformation under applied loads.
For example, in the design of beams, the moment of inertia determines the beam’s ability to withstand bending without collapsing. Similarly, in the design of columns, the moment of inertia influences the column’s resistance to buckling under compressive loads.
Moment of Inertia and Rotational Motion
Moment of inertia plays a crucial role in understanding the rotational motion of objects. It quantifies an object’s resistance to changes in its angular velocity. A higher moment of inertia indicates greater resistance to angular acceleration.
Moment of Inertia and Angular Acceleration
The relationship between moment of inertia (I) and angular acceleration (α) is expressed by the equation: τ = Iα, where τ represents the torque applied to the object. This equation demonstrates that the angular acceleration of an object is inversely proportional to its moment of inertia.
Objects with larger moments of inertia will experience smaller angular accelerations when subjected to the same torque.
Examples of Moment of Inertia Influence
- Spinning Tops:Spinning tops with larger moments of inertia will spin for longer durations due to their increased resistance to changes in angular velocity.
- Figure Skating:Figure skaters adjust their moment of inertia by extending or contracting their limbs. A larger moment of inertia makes it easier to spin at a slower angular velocity, providing more control and stability.
- Flywheels:Flywheels store energy by virtue of their high moment of inertia. They can be used to regulate the speed of machinery or provide backup power during power outages.
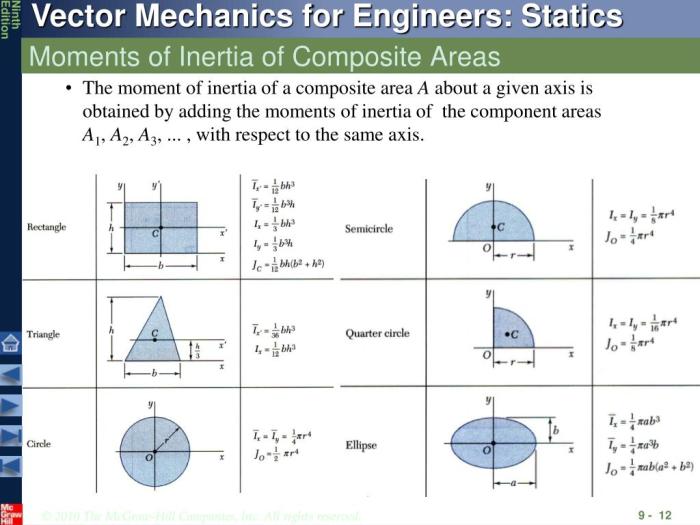
Comparison with Other Geometric Shapes
The moment of inertia of a trapezium can vary significantly compared to other geometric shapes due to differences in their mass distribution and shape. Let’s compare the moment of inertia of a trapezium with rectangles and triangles.
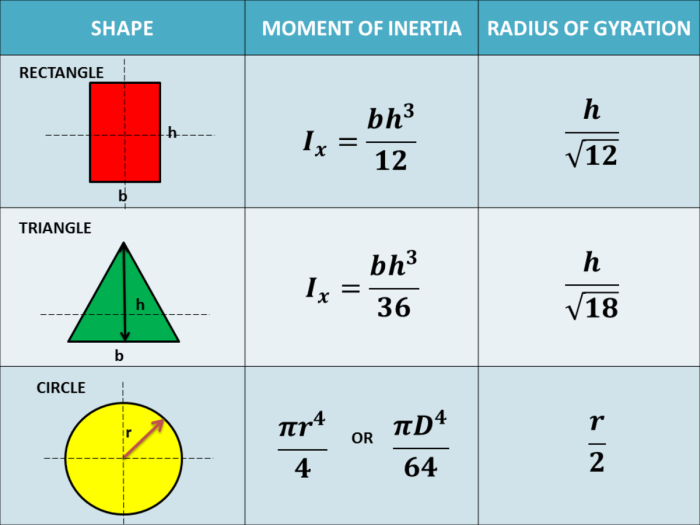
Rectangles
- Rectangles have a uniform mass distribution, resulting in a relatively high moment of inertia compared to trapeziums.
- The moment of inertia of a rectangle is proportional to the square of its width and height.
Triangles, Moment of inertia of trapezium
- Triangles have a non-uniform mass distribution, with the majority of the mass concentrated towards the base.
- The moment of inertia of a triangle is proportional to the square of its height and the cube of its base.
In general, the moment of inertia of a trapezium falls between that of a rectangle and a triangle, depending on the specific dimensions and mass distribution.
| Shape | Moment of Inertia |
|---|---|
| Rectangle | $I = \frac112 m (b^2 + h^2)$ |
| Triangle | $I = \frac118 m h^2 b$ |
| Trapezium | $I = \frac112 m (b_1^2 + b_2^2 + h^2)$ |
where:
- $m$ is the mass
- $b_1$ and $b_2$ are the lengths of the parallel sides
- $h$ is the height
FAQ Section
What is the formula for the moment of inertia of a trapezium?
The formula for the moment of inertia of a trapezium is (1/12) – m – (b1^2 + b2^2 + h^2), where m is the mass, b1 and b2 are the lengths of the parallel sides, and h is the height.
How is the moment of inertia used in engineering?
The moment of inertia is used in engineering to calculate the stability and strength of structures, such as bridges and buildings. It is also used to design rotating machinery, such as flywheels and turbines.
What is the relationship between moment of inertia and rotational motion?
The moment of inertia is directly proportional to the angular acceleration of an object. This means that objects with a higher moment of inertia will resist changes in their angular velocity more than objects with a lower moment of inertia.